| –Р–≤—В–Њ—А |
–°–Њ–Њ–±—Й–µ–љ–Є–µ |
CorvusCorax
–Р–≤—В–Њ—А —Б–∞–є—В–∞
ѕисьмо
|
# –Ф–∞—В–∞: 14 –Ь–∞—А 2020 14:13
–Э–∞ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–љ–Њ–є –Ї–∞—А—В–Њ—З–Ї–µ - —В—А–Є –Є–Љ–µ–љ–Є. –Ъ–∞–ґ–і–Њ–є –±—Г–Ї–≤–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Њ–і–љ–∞ —Г–љ–Є–Ї–∞–ї—М–љ–∞—П —Ж–Є—Д—А–∞ –Њ—В 0 –і–Њ 9, –≥–і–µ –Ј–∞—А–∞–љ–µ–µ –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ D=5. –Э–∞–є–і–Є—В–µ –Њ—Б—В–∞–ї—М–љ—Л–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є—П –±—Г–Ї–≤ –Є —Ж–Є—Д—А, —Б–ї–µ–і—Г—П –≤—Б–µ–Љ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –њ—А–∞–≤–Є–ї–∞–Љ —Б–ї–Њ–ґ–µ–љ–Є—П:

|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 14 –Ь–∞—А 2020 15:02 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
–≠—В–Њ –ї–µ–≥–Ї–Њ. –Я—А–Њ–Є—Б—Е–Њ–і–Є—В —Б—Г–Љ–Љ–Є—А–Њ–≤–∞–љ–Є–µ, –Є—В–∞–Ї –љ–∞—З–љ–µ–Љ —А–∞—Б—Б—Г–ґ–і–∞—В—М. D —А–∞–≤–љ–Њ 5. –Т—Л–і–µ–ї–Є–Љ –µ—С.
DONAL[D]+GERAL[D]=ROBER[0] 5+5=10 (–љ–Њ–ї—М –њ–Є—И–µ–Љ, 1 –≤ —Г–Љ–µ)
–Х–і–Є–љ–Є—Ж–∞ —А–∞–Ј—Г–Љ–µ–µ—В—Б—П –њ–µ—А–µ–Љ–µ—Б—В–Є–ї–∞—Б—М –≤–ї–µ–≤–Њ, —В–∞–Ї –Ї–∞–Ї —Б—Г–Љ–Љ–∞ –і–≤—Г—Е –Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е —З–Є—Б–µ–ї –≤—Б–µ–≥–і–∞ —З–µ—В–љ–Њ–µ —З–Є—Б–ї–Њ, —В–Њ –њ—А–Є +1, R —Г–ґ–µ –љ–µ—З–µ—В–љ–Њ–µ.
–Т –љ–∞—И–µ–Љ —Б–ї—Г—З–∞–µ –Њ—Б—В–∞—О—В—Б—П 7 –Є–ї–Є 9 (—Н—В–Њ –љ–∞–і–Њ –Ј–∞–њ–Њ–Љ–љ–Є—В—М). –Я–Њ–≥–љ–∞–ї–Є –і–∞–ї–µ–µ O+E=O. –Ґ–∞–Ї–Њ–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤ –і–≤—Г—Е —Б–ї—Г—З–∞—П—Е, –Ї–Њ–≥–і–∞ E=0 –ї–Є–±–Њ E=9, –∞ –µ–і–Є–љ–Є—Ж–∞ —Б–Љ–µ—Й–∞–µ—В—Б—П –Њ–њ—П—В—М –≤–ї–µ–≤–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г T —Г–ґ–µ —А–∞–≤–љ–Њ 0, —В–Њ –Ј–љ–∞—З–Є—В E=9. –Ь—Л –њ–Њ–Љ–љ–Є–Љ, —З—В–Њ R –љ–µ—З–µ—В–љ–Њ–µ –Є R –±–Њ–ї—М—И–µ 5, —В.–Ї. –≤ –њ–µ—А–≤–Њ–Љ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–Љ —А—П–і—Г G –њ—А–Є–±–∞–≤–ї—П–µ—В—Б—П –Ї –њ—П—В–µ—А–Ї–µ. –Ґ–∞–Ї–Є—Е —З–Є—Б–µ–ї –≤—Б–µ–≥–Њ –і–≤–∞, 7 –Є 9. –Ю–њ—П—В—М –ґ–µ, –і–µ–≤—П—В–Ї–∞ —Г –±—Г–Ї–≤—Л E, —В–Њ R=7. G = 7 - 5 - 1 (–µ–і–Є–љ–Є—Ж–∞ –Њ—В —Б–ї–Њ–ґ–µ–љ–Є—П O+E) = 1 (G=1). –Ю–±—А–∞—В–Є–Љ –≤–Ј–Њ—А –љ–∞ L, —В—Г—В 2 –≤–∞—А–Є–∞–љ—В–∞, –Є–ї–Є 3+3, –Є–ї–Є 8+8 (–µ–і–Є–љ–Є—Ж–∞ –Њ—В —Б—Г–Љ–Љ—Л –њ–Њ—Б–ї–µ–і–љ–Є—Е –і–≤—Г—Е D). –°—Г–Љ–Љ–∞ –і–≤—Г—Е —З–µ—В–љ—Л—Е —З–Є—Б–µ–ї –і–∞–µ—В —В–∞–Ї–ґ–µ —З—С—В–љ–Њ–µ, –∞ E —Г –љ–∞—Б —В–Њ —А–∞–≤–љ–Њ 9. –Ґ–Њ –њ–Њ–ї—Г—З–∞–µ—В—Б—П –≤—В–Њ—А–Њ–є –≤–∞—А–Є–∞–љ—В. 8+8 (L=8). –Ф–ї—П A –Њ–њ—П—В—М –ґ–µ –≤–∞—А–Є–∞–љ—В–∞, (A+A+1) —А–∞–≤–љ–Њ 9 –ї–Є–±–Њ 19. –≤ –њ–µ—А–≤–Њ–Љ = (9-1)/2=4, –≤—В–Њ—А–Њ–є (19-1)/2=9, –і–µ–≤—П—В–Ї—Г —Г–і–∞–ї–Є–Љ, —В.–Ї. –Њ–љ–∞ —Г –±—Г–Ї–≤—Л E. –Ч–љ–∞—З–Є—В A=4. –Ь—Л –љ–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є —В—А–Њ–є–Ї—Г, –і–≤–Њ–є–Ї—Г –Є —И–µ—Б—В–µ—А–Ї—Г. –Ш—Б—Е–Њ–і—П –Є–Ј –љ–Є—Е –Њ–њ—А–µ–і–µ–ї—П–µ–Љ —Б—Г–Љ–Љ—Г –і–ї—П N+R. x+7=y, 3+7=10 (–љ–Њ–ї—М —Г–ґ–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є), –Ј–љ–∞—З–Є—В –љ–µ –њ–Њ–і—Е–Њ–і–Є—В. –Ю—Б—В–∞–µ—В—Б—П 6. 6+7=13 (3, 1 –≤ —Г–Љ–µ). –Ю—Б—В–∞–ї–∞—Б—М –і–≤–Њ–є–Ї–∞, –Ї–Њ—В–Њ—А–∞—П –∞–≤—В–Њ–Љ–∞—В–Є—З–µ—Б–Ї–Є –њ–µ—А–µ–љ–Њ—Б–Є—В—Б—П –Ї –±—Г–Ї–≤–µ O. –Т—Б—С!
D=5, O=2, N=6, A=4, L=8, G=1, E=9, R=7, B=3, T=0
|
Date84
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Land of the Rising Sun
|
# –Ф–∞—В–∞: 14 –Ь–∞—А 2020 15:13 - –Я–Њ–њ—А–∞–≤–Є–ї: Date84
isamegrelo
–Х–і–Є–љ–Є—Ж–∞ —А–∞–Ј—Г–Љ–µ–µ—В—Б—П –њ–µ—А–µ–Љ–µ—Б—В–Є–ї–∞—Б—М –≤–ї–µ–≤–Њ, —В–∞–Ї –Ї–∞–Ї —Б—Г–Љ–Љ–∞ –і–≤—Г—Е –Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е —З–Є—Б–µ–ї –≤—Б–µ–≥–і–∞ —З–µ—В–љ–Њ–µ —З–Є—Б–ї–Њ, —В–Њ –њ—А–Є +1, R —Г–ґ–µ –љ–µ—З–µ—В–љ–Њ–µ.
–Т—Б—С —В–∞–Ї–Є —П —В—Г–њ–Њ–є. –Ъ–Њ–≥–і–∞ —Б–ї–Њ–ґ–Є–ї 5+5 - –њ–Њ–ї—Г—З–Є–ї–Њ—Б—М 10, —П –њ–Њ–і—Г–Љ–∞–ї —З—В–Њ –љ–µ —В–Њ, —В.–Ї. —З–Є—Б–ї–∞ –Њ—В 1 –і–Њ 9. –Я–Њ—В–Њ–Љ –њ—Л—В–∞–ї—Б—П –і–µ–ї–Є—В—М, –Є —Б–љ–Њ–≤–∞ –љ–Є—З–µ–≥–Њ –љ–µ –њ–Њ–ї—Г—З–Є–ї–Њ—Б—М. –У–ї–∞–≤–љ–Њ–µ —З—В–Њ-–±—Л —Н—В–Њ –љ–µ –њ—А–Њ—З–Є—В–∞–ї –Љ–Њ–є –љ–∞—З–∞–ї—М–љ–Є–Ї.))
|
CorvusCorax
–Р–≤—В–Њ—А —Б–∞–є—В–∞
ѕисьмо
|
# –Ф–∞—В–∞: 14 –Ь–∞—А 2020 17:34

–ѓ —Н—В—Г –Ј–∞–і–∞—З—Г —А–µ—И–∞–ї –≥–Њ–і –Є–ї–Є –і–≤–∞ –љ–∞–Ј–∞–і, —А–µ—И–µ–љ–Є–µ –Ј–∞–љ—П–ї–Њ –љ–µ 15 –Љ–Є–љ—Г—В, –∞ 35 –Є–ї–Є 30 :)
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 14 –Ь–∞—А 2020 23:11
–°–Ї–Њ—А–µ–µ –і–ї—П —И–Ї–Њ–ї—М–љ–Є–Ї–Њ–≤ 3-4-–≥–Њ –Ї–ї–∞—Б—Б–∞ –Ј–∞–і–∞—З–Ї–∞. –Т—Б–µ —З—В–Њ –љ—Г–ґ–љ–Њ –њ–Њ–Љ–љ–Є—В—М —Н—В–Њ –њ—А–∞–≤–Є–ї–∞ —Б–ї–Њ–ґ–µ–љ–Є—П –≤ —Б—В–Њ–ї–±–Є–Ї.
|
CorvusCorax
–Р–≤—В–Њ—А —Б–∞–є—В–∞
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 07:44
Sanek06
–Э—Г –Ї–Њ–љ–µ—З–љ–Њ, –≤—Л –ґ–µ —Г –љ–∞—Б –≥–µ–љ–Є–є –Є –≤—Г–љ–і–µ—А–Ї–Є–љ–і.
–Э–∞ —Б–∞–є—В–µ, –Њ—В–Ї—Г–і–∞ —П —Б–Ї–Њ–њ–Є—А–Њ–≤–∞–ї —Н—В—Г –Ј–∞–і–∞—З—Г, –≤–Ј—А–Њ—Б–ї—Л–µ –Љ—Г–ґ–Є–Ї–Є —Б –≤—Л—Б—И–Є–Љ —В–µ—Е–љ–Є—З–µ—Б–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ–Љ –Є –±–Њ–ї—М—И–Є–Љ –Њ–њ—Л—В–Њ–Љ —А–∞–±–Њ—В—Л –љ–∞ —А–µ—И–µ–љ–Є–µ —Н—В–Њ–є –Ј–∞–і–∞—З–Є –њ–Њ—В—А–∞—В–Є–ї–Є –Њ—В 13 –і–Њ 20 –Љ–Є–љ—Г—В –Є –±–Њ–ї–µ–µ.
|
CorvusCorax
–Р–≤—В–Њ—А —Б–∞–є—В–∞
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 17:24
–Х—Й—С –Ј–∞–і–∞—З–∞ (–Є–Ј —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–≥–Њ —Г—З–µ–±–љ–Є–Ї–∞ –∞–ї–≥–µ–±—А—Л –Ј–∞ 7 –Ї–ї–∞—Б—Б).
–Т –ї–∞–≥–µ—А—М –њ—А–Є–µ—Е–∞–ї–Є —В—А–Є –Љ–∞–ї—М—З–Є–Ї–∞ - –С—Г—А–Њ–≤, –У—А–Є–і–љ–µ–≤ –Є –Ъ–ї–Є–Љ–µ–љ–Ї–Њ.
–Ч–Њ–≤—Г—В –Є—Е –Ъ–Њ–ї—П, –Я–µ—В—П –Є –У—А–Є—И–∞.
–Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ:
1. –С—Г—А–Њ–≤ –љ–µ –Ъ–Њ–ї—П.
2. –†–Њ–і–љ–Њ–є –±—А–∞—В –Љ–∞—В–µ—А–Є –С—Г—А–Њ–≤–∞ –Є–Љ–µ–µ—В —Д–∞–Љ–Є–ї–Є—О –°–µ—А–Њ–≤.
3. –Я–µ—В—П –њ–Њ—И–µ–ї –≤ —И–Ї–Њ–ї—Г 7 –ї–µ—В –Є —Г—З–Є—В—Б—П —Е–Њ—А–Њ—И–Њ. –Т –њ–Є—Б—М–Љ–µ –Њ–љ –њ–Є—И–µ—В:
¬Ђ...–Э–∞–Ї–Њ–љ–µ—Ж-—В–Њ –≤ —Н—В–Њ–Љ –≥–Њ–і—Г —П –љ–∞—З–љ—Г –Є–Ј—Г—З–∞—В—М –∞–ї–≥–µ–±—А—Г, –≥–µ–Њ–Љ–µ—В—А–Є—О, —Д–Є–Ј–Є–Ї—Г...¬ї.
4. –°–∞–і–Њ–≤–љ–Є–Ї –ї–∞–≥–µ—А—П –°–µ–Љ–µ–љ –Ч–∞—Е–∞—А–Њ–≤–Є—З –Ь–Њ–Ї—А–Њ—Г—Б–Њ–≤ –њ—А–Є—Е–Њ–і–Є—В—Б—П –Я–µ—В–µ —А–Њ–і–љ—Л–Љ –і–µ–і—Г—И–Ї–Њ–є –Є –Њ—З–µ–љ—М —А–∞–і –њ—А–Є–µ–Ј–і—Г –≤–љ—Г–Ї–∞.
5. –У—А–Є–і–љ–µ–≤ —Б—В–∞—А—И–µ –Я–µ—В–Є –љ–∞ 1 –≥–Њ–і.
6. –У—А–Є—И–∞ —Б—В–∞—А—И–µ –Я–µ—В–Є –љ–∞ 1 –≥–Њ–і.
–£—Б—В–∞–љ–Њ–≤–Є—В–µ –Є–Љ—П –Є –≤–Њ–Ј—А–∞—Б—В –Ї–∞–ґ–і–Њ–≥–Њ –Љ–∞–ї—М—З–Є–Ї–∞.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 18:58 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
–Э–Є–Ї–Њ–ї–∞–є –љ–µ –С—Г—А–Њ–≤ (–Ј–љ–∞—З–Є—В –У—А–Є–і–љ–µ–≤ –Є–ї–Є –Ъ–ї–Є–Љ–µ–љ–Ї–Њ). –£ –Љ–∞–Љ—Л –С—Г—А–Њ–≤–∞ —Д–∞–Љ–Є–ї–Є—П –°–µ—А–Њ–≤–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —А–Њ–і–љ–Њ–є –±—А–∞—В —Б —В–∞–Ї–Њ–є —Д–∞–Љ–Є–ї–Є–µ–є. –Ь–Њ–Ї—А–Њ—Г—Б–Њ–≤ –њ—А–Є—Е–Њ–і–Є—В—Б—П –Њ—В—Ж–Њ–Љ –Љ–∞–Љ—Л –Я–µ—В—А–∞, –њ–Њ–ї—Г—З–∞–µ—В—Б—П —Г –љ–µ–≥–Њ —Д–∞–Љ–Є–ї–Є—П –Ъ–ї–Є–Љ–µ–љ–Ї–Њ –Є–ї–Є –С—Г—А–Њ–≤. –Э–∞ –і–∞–љ–љ—Л–є –Љ–Њ–Љ–µ–љ—В –Є–Љ–µ–µ—В –і–≤–∞ —Д–∞–Ї—В–∞: –Љ–∞–Љ–∞ –Я–µ—В—А–∞ > –Ь–Њ–Ї—А–Њ—Г—Б–Њ–≤–∞, –∞ –С—Г—А–Њ–≤–∞ > –°–µ—А–Њ–≤–∞. –Ш–Ј —Н—В–Њ–≥–Њ –≤—Л—В–µ–Ї–∞–µ—В, —З—В–Њ –Я–µ—В—А –Ъ–ї–Є–Љ–µ–љ–Ї–Њ. –Ш–і–µ—В –≤–Ј–∞–Є–Љ–Њ–Є—Б–Ї–ї—О—З–µ–љ–Є–µ –Є –∞–≤—В–Њ–Љ–∞—В–Є—З–µ—Б–Ї–Є —Д–∞–Љ–Є–ї–Є—П –С—Г—А–Њ–≤ –њ–µ—А–µ—Е–Њ–і–Є—В –Ї –У—А–Є–≥–Њ—А–Є—О. –Ю—Б—В–∞–ї–∞—Б—М –Њ–і–љ–∞ —Д–∞–Љ–Є–ї–Є—П - –У—А–Є–і–љ–µ–≤, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –і–≤—Г–Љ —Д–∞–Љ–Є–ї–Є—О —Г–ґ–µ –њ—А–Њ–њ–Є—Б–∞–ї, —В–Њ –Њ—Б—В–∞–ї—Б—П –Њ–і–Є–љ –Э–Є–Ї–Њ–ї–∞–є. –І—В–Њ –Ї–∞—Б–∞–µ—В—Б—П –≤–Њ–Ј—А–∞—Б—В–∞, —В–Њ –љ–∞–і–Њ –Ј–љ–∞—В—М –≤ –Ї–∞–Ї–Њ–Љ –Ї–ї–∞—Б—Б–µ –љ–∞—З–Є–љ–∞—О—В –Є–Ј—Г—З–∞—В—М —Д–Є–Ј–Є–Ї—Г. –£ –љ–∞—Б –Њ–љ–∞ –±—Л–ї–∞ —Б 7 –Ї–ї–∞—Б—Б–∞. –Ч–љ–∞—З–Є—В –≤–Њ–Ј—А–∞—Б—В –Я–µ—В—А–∞ - 14 –ї–µ—В, –∞ –µ–≥–Њ 2 –і—А—Г–≥–∞ —Б—В–∞—А—И–µ –љ–∞ 1 –≥–Њ–і - 15 –ї–µ—В.
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 18:59 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
CorvusCorax
–Я–Њ—В–Њ–Љ—Г —З—В–Њ –Љ–љ–Њ–≥–Є–µ –Ј–∞–±—Л–≤–∞—О—В –њ—А–∞–≤–Є–ї–∞ —Б—З–µ—В–∞ –≤ —Б—В–Њ–ї–±–Є–Ї. –≠—В–Њ –µ–і–Є–љ—Б—В–≤–µ–љ–љ–∞—П –≤–Њ–Ј–Љ–Њ–ґ–љ–∞—П –њ—А–Њ–±–ї–µ–Љ–∞ –њ—А–Є —А–µ—И–µ–љ–Є–Є. –ѓ –њ–Њ—В—А–∞—В–Є–ї –љ–∞ –љ–µ–µ 5 –Љ–Є–љ—Г—В(—А–µ—И–Є–≤ –њ–Њ–ї–Њ–≤–Є–љ—Г –≥–і–µ-—В–Њ, –і–∞–ї—М—И–µ —Б—В–∞–ї–Њ –љ–µ–Є–љ—В–µ—А–µ—Б–љ–Њ –Ј–∞–љ–Є–Љ–∞—В—М—Б—П —А—Г—В–Є–љ–љ—Л–Љ–Є —В—А–Є–≤–Є–∞–ї—М–љ—Л–Љ–Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П–Љ–Є), –љ–Њ, —Б–µ–є—З–∞—Б, –њ—А–∞–≤–і–∞, —П –Ј–∞–љ–Є–Љ–∞—О—Б—М –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–є –Њ—З–µ–љ—М –њ–ї–Њ—В–љ–Њ...
–Ф–∞ –Є –њ—А–Є—З–µ–Љ –Ј–і–µ—Б—М –≤—Г–љ–і–µ—А–Ї–Є–љ–і? –≠—В–Њ –њ—А–Њ—Б—В–Њ —Б–Љ–µ—И–љ–Њ –Є –љ–µ–ї–µ–њ–Њ. –Ф—Г–Љ–∞—О, –љ–Њ—А–Љ–∞–ї—М–љ–Њ –Њ—В—Г—З–Є–≤—И–Є–є—Б—П —В–µ—Е–љ–∞—А—М —А–µ—И–Є—В –µ–µ –Ј–∞ –њ–∞—А—Г –Љ–Є–љ—Г—В –µ—Б–ї–Є –љ–µ –±—Л—Б—В—А–µ–µ. –Ґ–Њ —З—В–Њ –Ї–∞–Ї–Є–µ-—В–Њ –Љ—Г–ґ–Є–Ї–Є —А–µ—И–∞—О—В –Ј–∞ 20 –Љ–Є–љ—Г—В - –љ–µ –Њ —З–µ–Љ.
–≠—В–∞ –Ј–∞–і–∞—З–Ї–∞ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–∞—П –Є –љ–Є–Ї–∞–Ї–Є–Љ —В–µ—Е–љ–Є—З–µ—Б–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –љ–µ –љ—Г–ґ–љ–Њ –Њ–±–ї–∞–і–∞—В—М —З—В–Њ–±—Л –µ–µ —А–µ—И–Є—В—М, —В–µ–Љ –±–Њ–ї–µ–µ –±—Л—В—М –≤—Г–љ–і–µ—А–Ї–Є–љ–і–Њ–Љ –Є –і–∞–ґ–µ –њ—А–Њ—Б—В–Њ —Г–Љ–љ—Л–Љ.
–Т–Њ—В –Ј–і–µ—Б—М –±–Њ–ї–µ–µ —А–µ–∞–ї—М–љ—Л–µ –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ –Љ–Њ–≥—Г—В –±—Л—В—М –љ–∞ –Є–љ—В–µ—А–≤—М—О —Г —В–µ—Е–љ–∞—А–µ–є –≤ —В–∞–Ї–Є—Е –Ї–Њ–Љ–њ–∞–љ–Є—П:
https://youtu.be/IMlrNbK4JGI
–Ъ–Њ–љ–µ—З–љ–Њ —Д–Њ—А–Љ–∞—В –љ–µ —Б–Њ–≤—Б–µ–Љ —Г–і–Њ–±–љ—Л–є, –љ–Њ –њ—А–Є –њ–µ—А–µ–Љ–Њ—В–Ї–µ –Ј–∞–і–∞—З–Є –Љ–µ—Б—В–∞–Љ–Є –≥–Њ–і–љ—Л–µ –Є —В—Г—В –ґ–µ –Љ–Њ–ґ–љ–Њ —Г–≤–Є–і–µ—В—М –Ї–∞–Ї —В–µ—Е–љ–∞—А—М —А–µ—И–∞–µ—В –≤ —А–∞–Ј—Л –±–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ—Л–µ –Ј–∞–і–∞—З–Є.
|
CorvusCorax
–Р–≤—В–Њ—А —Б–∞–є—В–∞
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 19:23
–≠—В–Њ –њ—А–Њ—Б—В–Њ —Б–Љ–µ—И–љ–Њ –Є –љ–µ–ї–µ–њ–Њ.
Sanek06
–°–Љ–µ—И–љ–Њ –Є –љ–µ–ї–µ–њ–Њ –≤–∞—И–µ —Е–≤–∞—Б—В–Њ–≤—Б—В–≤–Њ.
–Т–Њ –≤—А–µ–Љ–µ–љ–∞ –§–Њ—А–і–∞ –і–ї—П –≤–Ј—А–Њ—Б–ї—Л—Е –ї—О–і–µ–є —Б—З–Є—В–∞–ї–Њ—Б—М –і–Њ–±–ї–µ—Б—В—М—О —А–µ—И–Є—В—М —Н—В—Г –Ј–∞–і–∞—З—Г –Ј–∞ 15 –Љ–Є–љ—Г—В, –і–∞ –Є —Б–µ–є—З–∞—Б —В–Њ–ґ–µ —В–∞–Ї (—Б—Г–і—П –њ–Њ –Њ–њ—Л—В—Г –Є –Њ—В–Ј—Л–≤–∞–Љ —А–µ—И–∞–≤—И–Є—Е).
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 19:24 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
CorvusCorax
–Т–Њ –≤—А–µ–Љ–µ–љ–∞ –§–Њ—А–і–∞ –і–ї—П –≤–Ј—А–Њ—Б–ї—Л—Е –ї—О–і–µ–є —Б—З–Є—В–∞–ї–Њ—Б—М –і–Њ–±–ї–µ—Б—В—М—О —А–µ—И–Є—В—М —Н—В—Г –Ј–∞–і–∞—З—Г –Ј–∞ 15 –Љ–Є–љ—Г—В
–°—Б—Л–ї–Ї—Г –љ–∞ –њ–µ—А–≤–Њ–Є—Б—В–Њ—З–љ–Є–Ї –Љ–Њ–ґ–µ—В–µ –њ—А–µ–і–Њ—Б—В–∞–≤–Є—В—М —З—В–Њ –њ–Њ–і–Њ–±–љ–∞—П –Ј–∞–і–∞—З–∞ –±—Л–ї–∞ –љ–∞ –Є–љ—В–µ—А–≤—М—О —Г –Є–љ–ґ–µ–љ–µ—А–Њ–≤ –≤ –§–Њ—А–і–µ? –Т—Л –њ–Њ–љ–Є–Љ–∞–µ—В–µ —З—В–Њ —Н—В–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–∞—П –±–∞—Б–љ—П –Ї–Њ–Є—Е —А–∞—Б–њ–ї–Њ–і–Є–ї–Њ—Б—М –≤ –Є–љ—В–µ—А–љ–µ—В–µ —В—Л—Б—П—З–Є, –љ–∞ –њ–Њ–і–Њ–±–Є–µ –Ч–∞–і–∞—З–Є –љ–∞ IQ –Њ—В –≠–є–љ—И—В–µ–є–љ–∞ –Є –њ—А–Њ—З–µ–≥–Њ –Љ–Є—Д–Њ—В–≤–Њ—А—З–µ—Б—В–≤–∞. –Я–Њ —Д–∞–Ї—В—Г –ґ–µ,99.9% –≤–Ј—П—В–∞—П –Є–Ј —Б–±–Њ—А–љ–Є–Ї–∞ –Ј–∞–і–∞—З–µ–Ї –љ–∞ –ї–Њ–Ї–Є–Ї—Г –і–ї—П —И–Ї–Њ–ї—М–љ–Є–Ї–Њ–≤ –Є –њ—А–Њ—З–Є—Е –Є–љ—В–µ—А–µ—Б—Г—О—Й–Є—Е—Б—П(—В–∞–Ї–ґ–µ, –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, —Б–µ–є—З–∞—Б –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –љ–∞ –Є–љ—В–µ—А–≤—М—О —Г –љ–∞—З–Є–љ–∞—О—Й–Є—Е –њ—А–Њ–≥—А–∞–Љ–Љ–Є—Б—В–Њ–≤).
–Ш –Њ—В–Ї—Г–і–∞ —Г –Т–∞—Б –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П –њ—А–Њ —В–Њ –Ї–∞–Ї —А–µ—И–∞–ї–∞—Б—М —Н—В–∞ –Ј–∞–і–∞—З–∞ –Є–љ–ґ–µ–љ–µ—А–∞–Љ–Є –≤–Њ –≤—А–µ–Љ–µ–љ–∞ –§–Њ—А–і–∞? –Х—Б—В—М —Е–Њ—В—П –Ї–∞–Ї–Є–µ-—В–Њ –і–Њ–Ї—Г–Љ–µ–љ—В–∞–ї—М–љ—Л–µ —Б–≤–µ–і–µ–љ–Є—П?
|
Spasatel
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
–Ґ–∞–ї–і–Њ–Љ
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 19:25 - –Я–Њ–њ—А–∞–≤–Є–ї: Spasatel
CorvusCorax
{}
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 20:19 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
—П –Ј–∞–љ–Є–Љ–∞—О—Б—М –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–є –Њ—З–µ–љ—М –њ–ї–Њ—В–љ–Њ
Sanek06
–≠—В–Њ —Е–Њ—А–Њ—И–Њ. –Ь–Њ–ґ–љ–Њ –љ–∞–њ–Є—Б–∞—В—М –Љ–Њ—О –Ј–∞–і–∞—З—Г?
–Х—Б—В—М –і–≤–µ –Љ–∞—В—А–Є—Ж—Л:
[8, 5, 9; 12, 4, 7; 23, 28, 14]
[3, 7, 2; 8, 11, 6; 14, 21, 17]
1. –Э–∞–і–Њ —Б–і–µ–ї–∞—В—М –Є—Е —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–Є–µ
2. –Т –і–∞–ї—М–љ–µ–є—И–µ–Љ —Г–Ј–љ–∞—В—М –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ
3. –Я—А–Њ—Б—Г–Љ–Љ–Є—А–Њ–≤–∞—В—М –≤—Б–µ —Н–ї–µ–Љ–µ–љ—В—Л.
4. –°—Г–Љ–Љ—Г –≤–Њ–Ј–≤–µ—Б—В–Є –≤ —Б—В–µ–њ–µ–љ—М —З–Є—Б–ї–∞ –Є–Ј –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є–Є –†–Є–Љ–∞–љ–љ–∞ (x=e)
5. –Ш –≤ –Ї–Њ–љ—Ж–µ –Є–Ј –≤—Л—И–µ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ —З–Є—Б–ї–∞ –љ–∞–є—В–Є –њ–Њ–ї–Є–ї–Њ–≥–∞—А–Є—Д–Љ —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ -2.
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 21:16 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
isamegrelo
5. –Ш –≤ –Ї–Њ–љ—Ж–µ –Є–Ј –≤—Л—И–µ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ —З–Є—Б–ї–∞ –љ–∞–є—В–Є –њ–Њ–ї–Є–ї–Њ–≥–∞—А–Є—Д–Љ —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ -2.
–≤—Л—И–ї–Њ 150857.1834 –і–Њ 5.
C –њ–Њ–ї–Є–ї–Њ–≥–∞—А–Є—Д–Љ–∞–Љ–Є —П –љ–µ –Ј–љ–∞–Ї–Њ–Љ, —Б–µ–є—З–∞—Б –љ–µ—В –≤—А–µ–Љ–µ–љ–Є –љ–∞ —Н—В–Њ. –Э–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л–є –∞–љ–∞–ї–Є–Ј —Г–≤–ї–µ–Ї–∞—В–µ–ї—М–љ–∞—П –≤–µ—Й—М...
–µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–љ—Л–µ –Љ–∞—В—А–Є—Ж—Л —П –њ–µ—А–µ–Љ–љ–Њ–ґ–∞–ї –њ—А–Њ—Б—В–Њ –Ї–∞–Ї –Њ—В–і–µ–ї—М–љ—Л–µ —Н–ї–µ–Љ–µ–љ—В—Л –Љ–∞—Б—Б–Є–≤–Њ–≤ –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є(–≤-–≤–Є–і—Г –љ–µ—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є—П —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–µ–є –і–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –Њ–њ–µ—А–∞—Ж–Є–Є –≤ –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ) , –∞ –љ–µ –њ–Њ –њ—А–∞–≤–Є–ї–∞–Љ –ї–Є–љ–µ–є–љ–Њ–є –∞–ї–≥–µ–±—А—Л. –Э—Г –Є–ї–Є –Ї–∞–Ї-—В–Њ –±–Њ–ї–µ–µ –Ї–Њ—А—А–µ–Ї—В–љ–Њ –њ–Њ—Б—В–∞–≤—М—В–µ —Г—Б–ї–Њ–≤–Є—П(–ї–Є–±–Њ —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П, –ї–Є–±–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П), –ї–Є–±–Њ —Б–∞–Љ–Є –Љ–∞—В—А–Є—Ж—Л –і—А—Г–≥–Њ–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є...
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 22:08
Sanek06
–Т—Б–µ –њ—А–∞–≤–Є–ї—М–љ–Њ —П —Г–Ї–∞–Ј–∞–ї. –°–љ–∞—З–∞–ї–∞ —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–Є–µ, –∞ –њ–Њ—В–Њ–Љ —Г–Љ–љ–Њ–ґ–µ–љ–Є–µ –Љ–∞—В—А–Є—Ж.
–Ш—Б—Е–Њ–і–љ—Л–є –≤–Є–і:

|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 22:12 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
Sanek06
–ѓ —В–∞–Љ –і–Њ–±–∞–≤–Є–ї –ґ–µ —В–Њ—З–Ї—Г —Б –Ј–∞–њ—П—В–Њ–є) –Ъ–≤–∞–і—А–∞—В–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ 3-–≥–Њ –њ–Њ—А—П–і–Ї–∞.
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 22:16 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
isamegrelo
—В–Њ–≥–і–∞ 544991.09 –і–Њ 5.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 22:24
Sanek06
–Ю—В–≤–µ—В –љ–µ–њ—А–∞–≤–Є–ї—М–љ—Л–є. –Я–Њ—Б—В–∞—А–∞–є—В–µ—Б—М –љ–∞–є—В–Є –Њ—И–Є–±–Ї—Г. –Я–Њ—Б–ї–µ —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П –Љ. –њ—А–Є–љ–Є–Љ–∞–µ—В —В–∞–Ї–Њ–є –≤–Є–і:

|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 22:35 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
isamegrelo
–ѓ –≤ –Ї—Г—А—Б–µ –Ї–∞–Ї–Њ–є –≤–Є–і –Љ–∞—В—А–Є—Ж–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –њ–Њ—Б–ї–µ —В—А–∞–љ—Б–њ–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П. –£ –Љ–µ–љ—П —В–∞–Ї–∞—П –ґ–µ. –Э–∞–њ–Є—И–Є—В–µ –≤–∞—И–Є —А–∞—Б—З–µ—В—Л. —Б—А–∞–≤–љ–Є–Љ.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 23:15
Sanek06
8*3+12*7+23*2=154
5*3+4*7+28*2=99
9*3+7*7+14*2=104
8*8+12*11+23*6=334
5*8+4*11+28*6=252
9*8+7*11+14*6=233
8*14+12*21+23*17=755
5*14+4*21+28*17=630
9*14+7*21+14*17=511

–°—Г–Љ–Љ–∞ —Н–ї–µ–Љ–µ–љ—В–Њ–≤: 3072
–І–µ–Љ—Г —А–∞–≤–љ–∞ –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є—П –†–Є–Љ–∞–љ–∞ –Њ—В —З–Є—Б–ї–∞ –≠–є–ї–µ—А–∞?
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 15 –Ь–∞—А 2020 23:28
isamegrelo
–Э–∞—И–µ–ї —Б–≤–Њ—О –Њ—И–Є–±–Ї—Г. –Я—А–Є –Ї–Њ–њ–Є—А–Њ–≤–∞–љ–Є–Є —З–Є—Б–ї–∞ –љ–∞ —Б–∞–є—В–µ —А–∞–Ј–і–µ–ї–Є—В–µ–ї—М ., –∞ –љ–µ –Ј–∞–њ—П—В–∞—П. –Я–Њ—Н—В–Њ–Љ—Г –Љ–Њ–є –Њ—В–≤–µ—В –±—Л–ї –і–ї—П –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є x=2.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 00:04 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
Sanek06
–Я–Њ–≤—В–Њ—А—П—О –≤–Њ–њ—А–Њ—Б: —З–µ–Љ—Г —А–∞–≤–љ–∞ —Н—В–∞ —Б–∞–Љ–∞—П –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є—П –Њ—В e?
ζ(2.71828)= ?
–Х—Б–ї–Є —Н—В–Њ —Б–Љ–Њ–ґ–µ—В–µ –≤—Л—З–Є—Б–ї–Є—В—М, —В–Њ –≥–Њ—В–Њ–≤ –њ—А–Є–Ј–љ–∞—В—М, —З—В–Њ —Г –≤–∞—Б –Ј–љ–∞–љ–Є–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –љ–∞ –≤—Л—Б–Њ–Ї–Њ–Љ —Г—А–Њ–≤–љ–µ.

|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 06:13 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
isamegrelo
–≠—В–Њ —Г–ґ–µ –њ—А–µ–≤—А–∞—Й–∞–µ—В—Б—П –≤ –Ї–∞–Ї–Њ–µ-—В–Њ –њ–Њ–і–Њ–±–Є–µ —Б–∞–і–Њ–Љ–∞–Ј–Њ. –С—Г–і–µ–Љ —Б—З–Є—В–∞—В—М —З—В–Њ —П –Ј–∞—Д–µ–є–ї–Є–ї—Б—П –Є –љ–µ –њ–Њ–љ—П–ї –Ї–∞–Ї –њ–Њ–і—Б—З–Є—В–∞—В—М —Б—Г–Љ–Љ—Г –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞—О—Й–µ–≥–Њ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ–Њ–≥–Њ —А—П–і–∞(–љ–∞ –≤—Б—П–Ї–Є–є —Б–ї—Г—З–∞–є –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж–Є–Є https://keisan.casio.com/exec/system/1180573439, —А—П–і—Л:
<a href="https://www.emathhelp.net/calculators/calculus-2/series-calculator/?f=1%2Fn%5E2.71828&var=&a=1&b=inf," target="_blank" rel="nofollow">https://www.emathhelp.net/calculato rs/calculus-2/s eries-calculator/?f=1%2Fn%5E2.71828&var=&a=1&b=i nf,</a> –∞–≤–Њ—Б—М –Ї–Њ–Љ—Г –њ—А–Є–≥–Њ–і–Є—В—Б—П), –і–∞ –Є –≤ —Б–Є–ї—М–љ—Л–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є —П –љ–µ –Ј–∞–њ–Є—Б—Л–≤–∞–ї—Б—П... –њ–Њ–≥—А—Г–ґ–∞—О—Б—М –≤ –Њ–њ—В–Є–Љ–Є–Ј–∞—Ж–Є–Њ–љ–љ—Л–µ –Љ–µ—В–Њ–і—Л –њ–Њ —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В—Б–Ї–Њ–є –љ—Г–ґ–і–µ...
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 14:55 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
Sanek06
lim - –њ—А–µ–і–µ–ї –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є, N ->+∞ (–І–Є—Б–ї–Њ —Г—Б—В—А–µ–Љ–ї–µ–љ–љ–Њ–µ –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М)
N - –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–µ —З–Є—Б–ї–Њ, n - –љ–∞—З–∞–ї—М–љ–Њ–µ (n=1, —Б—В–∞—А—В –Њ—В –µ–і–Є–љ–Є—Ж—Л)
–°—А–∞–Ј—Г —И—В—Г—А–Љ–Њ–≤–∞—В—М –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М –љ–µ –±—Г–і–µ–Љ, –њ–Њ–Ї–∞ –Њ–±—Б–ї–µ–і—Г–µ–Љ —Д—А–∞–≥–Љ–µ–љ—В (–і–Њ 2 —З–Є—Б–µ–ї –њ–Њ—Б–ї–µ —В–Њ—З–Ї–Є)
–Т–Њ–Ј—М–Љ–µ–Љ –і–ї—П —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—П —З–Є—Б–ї–Њ 100 (N=100)
N^(1-s)/1-s=100^(1-2.71828)/(1-2.71828)=100^-1.71828/-1.71828=0.00036596537/-1.71828=-0.00021298354
N=100 Σ(1/n^s)=1/1^2.71828+1/2^2.71828+1/3^2.71828+1/4^2.71828+1/5^2.71828+1/6^2.71828+1/7^2.71828+1/8^2.71828+1/9^2.71828+1/10^2.71828+1/11^2.71828+1/12^2.71828+1/13^12.71828+1/14^2.71828+1/15^2.71828+1/16^2.71828+1/17^2.71828+1/18^2.71828+1/19^2.71828+1/20^2.71828+1/21^2.71828+1/22^2.71828+1/23^2.71828+1/24^2.71828+1/25^2.71828+1/26^2.71828+1/27^2.71828+1/28^2.71828+1/29^2.71828+1/30^2.71828+1/31^2.71828+1/32^2.71828+1/33^2.71828+1/34^2.71828+1/35^2.71828+1/36^2.71828+1/37^2.71828+1/38^2.71828+1/39^2.71828+1/40^2.71828+1/41^2.71828+1/42^2.71828+1/43^2.71828+1/44^2.71828+1/45^2.71828+1/46^2.71828+1/47^2.71828+1/48^2.71828+1/49^2.71828+1/50^2.71828+1/51^2.71828+1/52^2.71828+1/53^12.71828+1/54^2.71828+1/55^2.71828+1/56^2.71828+1/57^2.71828+1/58^2.71828+1/59^2.71828+1/60^2.71828+1/61^2.71828+1/62^2.71828+1/63^2.71828+1/64^2.71828+1/65^2.71828+1/66^2.71828+1/67^2.71828+1/68^2.71828+1/69^2.71828+1/70^2.71828+1/71^2.71828+1/72^2.71828+1/73^2.71828+1/74^2.71828+1/75^2.71828+1/76^2.71828+1/77^2.71828+1/78^2.71828+1/79^2.71828+1/80^2.71828+1/81^2.71828+1/82^2.71828+1/83^2.71828+1/84^2.71828+1/85^2.71828+1/86^2.71828+1/87^2.71828+1/88^2.71828+1/89^2.71828+1/90^2.71828+1/91^2.71828+1/92^2.71828+1/93^12.71828+1/94^2.71828+1/95^2.71828+1/96^2.71828+1/97^2.71828+1/98^2.71828+1/99^2.71828+1/100^2.71828=1.2678364073
n=1
–†—П–і –Љ–Њ–ґ–љ–Њ –њ—А–Њ–і–Њ–ї–ґ–Є—В—М –і–Њ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є, –љ–Њ 2 —З–Є—Б–ї–∞ –њ–Њ—Б–ї–µ —В–Њ—З–Ї–Є –Њ—Б—В–∞–љ—Г—В—Б—П –љ–µ–Є–Ј–Љ–µ–љ–љ—Л–Љ–Є!
Σ(1/n^s)-N^(1-s)/1-s=1.2678364073-(-0.00021298354) = 1.26804939084
–Ю–Ї—А—Г–≥–ї–Є–Љ –і–Њ 1.27
–Я–Њ—А–∞ –њ—А–Њ–≤–µ—А–Є—В—М –љ–∞ –≤–∞—И–µ–Љ –Ї–∞–ї—М–Ї—Г–ї—П—В–Њ—А–µ. ζ(2.71828)=1.26901012
–Ю–Ї—А—Г–≥–ї—П–µ—В—Б—П –Њ–њ—П—В—М –і–Њ 1.27
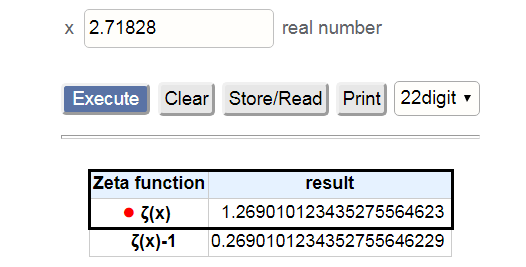
–Я–µ—А–µ—Е–Њ–і–Є–Љ –Ї –њ–Њ–ї–Є–ї–Њ–≥–∞—А–Є—Д–Љ—Г.
Li —Б –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ -2 –Њ—В x = x*(1+x)/(1-x)^3
x = 1.27
1.27*(1+1.27)/(1-1.27)^3=-146.466493929
–Ю–Ґ–Т–Х–Ґ: ~ -146.47
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 15:45 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
–Ч–∞–±—Л–ї –њ—А–Њ –≤—З–µ—А–∞—И–љ–Є–є 4-—Л–є –њ—Г–љ–Ї—В, —Б—Г–Љ–Љ—Г —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –≤–Њ–Ј–≤–µ—Б—В–Є –≤ —Б—В–µ–њ–µ–љ—М ζ(2.71828)
3072^1.27 = 26854.9865021 (~26855)
26855*(1+26855)/(1-26855)^3 = 721217880/(-26854)^3 = 721217880/-19365421483864 = -0.00003724256
–Ш—В–Њ–≥–Њ–≤—Л–є –Њ—В–≤–µ—В: -0.00003724256
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 20:14 - –Я–Њ–њ—А–∞–≤–Є–ї: Sanek06
isamegrelo
lim - –њ—А–µ–і–µ–ї –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є, N ->+∞ (–І–Є—Б–ї–Њ —Г—Б—В—А–µ–Љ–ї–µ–љ–љ–Њ–µ –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М)
N - –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–µ —З–Є—Б–ї–Њ, n - –љ–∞—З–∞–ї—М–љ–Њ–µ (n=1, —Б—В–∞—А—В –Њ—В –µ–і–Є–љ–Є—Ж—Л)
–°—А–∞–Ј—Г —И—В—Г—А–Љ–Њ–≤–∞—В—М –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М –љ–µ –±—Г–і–µ–Љ, –њ–Њ–Ї–∞ –Њ–±—Б–ї–µ–і—Г–µ–Љ —Д—А–∞–≥–Љ–µ–љ—В (–і–Њ 2 —З–Є—Б–µ–ї –њ–Њ—Б–ї–µ —В–Њ—З–Ї–Є)
–Т–Њ–Ј—М–Љ–µ–Љ –і–ї—П —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—П —З–Є—Б–ї–Њ 100 (N=100)
N^(1-s)/1-s=100^(1-2.71828)/(1-2.71828)=100^-1.718 28/-1.71828=0.00036596537/-1.71828=-0.00021298354
N=100 Σ(1/n^s)=1/1^2.71828+1/2^2.71828+1/3^2.71828+1/4^2.71828+1/5^2.71828+1/6^2.71828+1/7^2.71828+1/8^2.71828+1/9^2.71828+1/10^2.71828+1/11^2.71828+1/12^2.71828+1/13^12.71828+1/14^2.71828+1/15^2.71828+1/16^2.71828+1/17^2.71828+1/18^2.71828+1/19^2.71828+1/20^2.71828+1/21^2.71828+1/22^2.71828+1/23^2.71828+1/24^2.71828+1/25^2.71828+1/26^2.71828+1/27^2.71828+1/28^2.71828+1/29^2.71828+1/30^2.71828+1/31^2.71828+1/32^2.71828+1/33^2.71828+1/34^2.71828+1/35^2.71828+1/36^2.71828+1/37^2.71828+1/38^2.71828+1/39^2.71828+1/40^2.71828+1/41^2.71828+1/42^2.71828+1/43^2.71828+1/44^2.71828+1/45^2.71828+1/46^2.71828+1/47^2.71828+1/48^2.71828+1/49^2.71828+1/50^2.71828+1/51^2.71828+1/52^2.71828+1/53^12.71828+1/54^2.71828+1/55^2.71828+1/56^2.71828+1/57^2.71828+1/58^2.71828+1/59^2.71828+1/60^2.71828+1/61^2.71828+1/62^2.71828+1/63^2.71828+1/64^2.71828+1/65^2.71828+1/66^2.71828+1/67^2.71828+1/68^2.71828+1/69^2.71828+1/70^2.71828+1/71^2.71828+1/72^2.71828+1/73^2.71828+1/74^2.71828+1/75^2.71828+1/76^2.71828+1/77^2.71828+1/78^2.71828+1/79^2.71828+1/80^2.71828+1/81^2.71828+1/82^2.71828+1/83^2.71828+1/84^2.71828+1/85^2.71828+1/86^2.71828+1/87^2.71828+1/88^2.71828+1/89^2.71828+1/90^2.71828+1/91^2.71828+1/92^2.71828+1/93^12.71828+1/94^2.71828+1/95^2.71828+1/96^2.71828+1/97^2.71828+1/98^2.71828+1/99^2.71828+1/100^2.71828=1.2678364073
n=1
–Ґ–Њ–ї—М–Ї–Њ –Ј–∞—З–µ–Љ –љ—Г–ґ–љ–Њ –±—Л–ї–Њ —Н—В–Њ –і—Г–±–ї–Є—А–Њ–≤–∞—В—М, –њ—А–Њ—Б—В–Њ –і–µ—В–∞–ї–Є–Ј–Є—А—Г—П(–і–∞ –Є –≤—Л –ґ–µ –љ–µ –≤—А—Г—З–љ—Г—О —Н—В–Њ –њ–Є—Б–∞–ї–Є –Є –і–µ–ї–∞–ї–Є...–љ–∞–і–µ—О—Б—М)? –Х—Б–ї–Є —И–Њ, —П –љ–µ–Љ–љ–Њ–≥–Њ —В—А–Њ–ї–ї–Є–ї. –Ь–Њ—П —Б—Б—Л–ї–Ї–∞ –≤—А–Њ–і–µ –∞–Ї—В–Є–≤–љ–∞, —Б —Г–ґ–µ —Б –≤–±–Є—В—Л–Љ —З–Є—Б–ї–Њ–Љ e –Є –љ–∞–є–і–µ–љ–Њ–є –і–Ј–µ—В–∞ —Д—Г–љ–Ї—Ж–Є–Ї—Ж–Є–µ–є –±—Л–ї–∞...
–Я.–°. –Х—Б–ї–Є –≤—Л—П–≤–ї—П—В—М —Г—А–Њ–≤–µ–љ—М –≤–ї–∞–і–µ–љ–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–є —В–Њ –љ–∞ —Б–ї–Њ–ґ–љ—Л—Е –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е –Є –љ–µ—Б—В–∞–і–∞–љ–і–∞—А—В–љ—Л—Е(–Є –Є—В–µ—А–µ—Б–љ—Л—Е, —З—В–Њ–±—Л –љ–µ –±—Л–ї–Њ –ґ–∞–ї–Ї–Њ –њ–Њ—В—А–∞—З–µ–љ–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є)–Ј–∞–і–∞—З–∞—Е. –Т–∞—И—Г –Ј–∞–і–∞—З–Ї—Г –Ї–∞–Ї —В—А–Њ–ї–ї–Є–љ–≥ –≤–Њ—Б–њ—А–Є–љ–Є–Љ–∞—О –≤ –Ї–Њ–љ–Ї—В–µ–Ї—Б—В–µ –Њ—Ж–µ–љ–Ї–Є –Љ–∞—В. –Ј–љ–∞–љ–Є–є.
–•–Њ—В—П –Ї—В–Њ —Б —Е–Њ–і—Г —А–µ—И–∞–µ—В –њ–Њ –њ—А–Њ—И–µ—Б—В–≤–Є–Є –≥–Њ–і–∞ –њ–Њ—Б–ї–µ –≤—Б–µ—Е –Ј–∞—В—А–∞–≥–Є–≤–∞–µ–Љ—Л—Е –і–Є—Б—Ж–Є–њ–ї–Є–љ - –Љ–Є–љ–Є–Љ—Г–Љ —В—А–Њ–µ—З–љ–Є–Ї –≤ —В–µ—Е –≤—Г–Ј–µ, –љ–Њ —В–Њ–ї—М–Ї–Њ —Б —Е–Њ–і—Г, –Є–љ–∞—З–µ —Б–Љ—Л–ї–∞ 0.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 21:22 - –Я–Њ–њ—А–∞–≤–Є–ї: isamegrelo
–љ–∞ —Б–ї–Њ–ґ–љ—Л—Е –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е –Є –љ–µ—Б—В–∞–і–∞–љ–і–∞—А—В–љ—Л—Е –Ј–∞–і–∞—З–∞—Е
Sanek06
–Ы–∞–і–љ–Њ, –њ—Г—Б—В—М –±—Г–і–µ—В –±–Њ–ї—М—И–µ –њ—А–∞–≥–Љ–∞—В–Є–Ј–Љ–∞. –Э–∞ –Њ—Б–љ–Њ–≤–µ –≤—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е —Б–Љ–Њ–ґ–µ—В–µ –ї–Є –≤—Л –Њ–±—Г—З–Є—В—М –љ–µ–є—А–Њ–љ–љ—Г—О —Б–µ—В—М?
|
Sanek06
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 21:33
isamegrelo
–°–Љ–Њ–≥—Г –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ. –Э–Њ —Н—В–Њ —Б–Ї–Њ—А–µ–µ –Ї–∞—Б–∞–µ—В—Б—П —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞–љ–Є—П –±—Г–і–µ—В –љ–∞ –і–∞–љ–љ—Л–є –Љ–Њ–Љ–µ–љ—В.
–Э–Њ –Њ–њ—П—В—М –ґ–µ –Є–≥—А–∞—В—М—Б—П –≤ –њ—Б–µ–≤–і–Њ–≥—Г—А—Г –Є —Г—З–µ–љ–Є–Ї–∞ —П –љ–µ –±—Г–і—Г –љ–∞ —Н—В–Њ–Љ —Д–Њ—А—Г—Г–Љ–µ. –Я–Њ –Њ–Ї–Њ–љ—З–∞–љ–Є—О —Г–љ–Є–≤–µ—А–∞(–≤ –Є—О–ї–µ) –µ—Б–ї–Є –±—Г–і—Г—В –њ–Њ–і—Е–Њ–і—П—Й–Є–µ –≤–µ—В–Ї–Є –њ–Њ–њ—А–∞–Ї—В–Є–Ї—Г–µ–Љ—Б—П –љ–∞ –њ—А–Є–Ї–ї–∞–і–љ—Л—Е –≤–µ—Й–∞—Е —Б –Њ–±—К–µ–Ї—В–Є–≤–љ—Л–Љ –Є –Ї—А–Є—В–µ—А–Є—П–Љ–Є –Њ—Ж–µ–љ–Ї–Є - –љ–∞–њ—А–Є–Љ–µ—А –Ї–Њ–љ—В–µ–Ї—Б—В –љ–∞ Kaggle. –°–µ–є—З–∞—Б —Г –Љ–µ–љ—П –љ–µ—В –≤—А–µ–Љ–µ–љ–Є. –Ш –Ї—Б—В–∞–Є –і–Є–њ–ї–Њ–Љ —Г –Љ–µ–љ—П –њ–Њ –љ–µ–є—А–Њ–љ–Ї–µ –±—Г–і–µ—В.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 16 –Ь–∞—А 2020 21:49
Sanek06
–•–Њ—А–Њ—И–Њ!) –С—Г–і–µ–Љ –ґ–і–∞—В—М –ї–µ—В–Њ.
|
isamegrelo
–£—З–∞—Б—В–љ–Є–Ї
ѕисьмо
Zugdidi
|
# –Ф–∞—В–∞: 17 –Ь–∞—А 2020 18:22
–і–Є–њ–ї–Њ–Љ —Г –Љ–µ–љ—П –њ–Њ –љ–µ–є—А–Њ–љ–Ї–µ –±—Г–і–µ—В.
Sanek06
–Ю –≤–µ–ї–Є–Ї–Є–є –≥—Г—А—Г –њ–Њ –љ–µ–є—А–Њ–љ–Ї–∞–Љ, –Ї –Ї–∞–Ї–Њ–Љ—Г –≤–Є–і—Г –Њ—В–љ–Њ—Б–Є—В—Б—П –Э–° —Б —В–∞–Ї–Њ–є –∞—А—Е–Є—В–µ–Ї—В—Г—А–Њ–є?
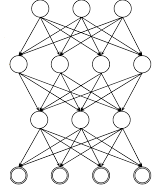
|